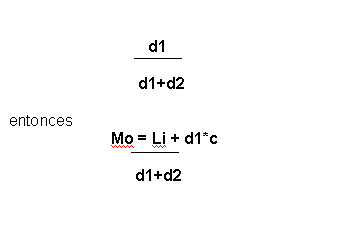
Otra medida de tendencia central es la moda, que como su nombre lo indica es aquel valor de la variable que muestra una mayor frecuencia o que más se repite.
Si la variable es continua, la moda ( o las modas ) corresponden a aquellos valores de la variable en los cuales la función alcanza un máximo relativo y habrá tantas modas como máximos relativos. Si el máximo es absoluto, la moda es única y se habla de "distribución unimodal". Si la función es uniforme (no hay máximo, entonces no existe moda)
EJEMPLOS :
1- La moda de los datos 2 3 3 3 5 8 es Mo=3
2- El conjunto de datos 1 2 2 2 2 4 5 6 6 6 6 7 tiene dos modas: Mo = 2 y Mo = 6, se dice que es una distribución bimodal.
3- Entre los datos 5 7.2 8 9 10.5 12 14 no existe moda
La moda de un conjunto de datos agrupados.
En una distribución de frecuencia la clase modal es la que tiene mayor frecuencia. Dicha frecuencia es la frecuencia modal.
Si d1 es la diferencia entre la frecuencia modal y la frecuencia de la clase anterior, d2 es la diferencia entre la frecuencia modal y la frecuencia de la clase posterior y c es el tamaño de los intervalos, el valor Mo de la moda se obtiene sumando el límite inferior de la clase modal el producto del tamaño de los intervalos por la fracción.
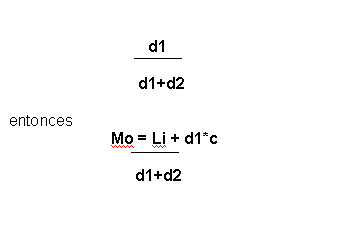
Ejemplo: Calculemos la moda para la siguiente distribución de puntajes de P.A.A.:
| PUNTAJE | fi |
|---|---|
| 350-399 | 4 |
| 400-499 | 6 |
| 450-499 | 9 |
| 500-549 | 20 |
| 550-599 | 31 |
| 600-649 | 80 |
| 650-699 | 42 |
| 700-749 | 10 |
| 750-799 | 8 |
| 800-849 | 2 |
La mayor frecuencia absoluta es 80 por lo tanto la clase es 600-949
El límite real inferior de la clase modal Li = 599.5
La frecuencia modal fi=80
D1=80-31=49
D2= 80-42=38
Tamaño Intervalo c= 50
Entonces, Mo =599.5+49*50 / 49+38
Mo=627.7=628 puntos
Se estima por tanto, que el valor más repetido de los puntajes de P.A.A. en estudio es aproximadamente 628 puntos.
Comparación entre Media, Mediana y Moda
- Si la distribución de frecuencias de la variable es simétrica las tres medidas coinciden.
- Si la distribución es unimodal y asimétrica positiva entonces Mo"nenor"Me"menor"X.
. - Si la distribución presenta asimetría negativa y es unimodal, entonces X"menor"Me"menor"Mo.