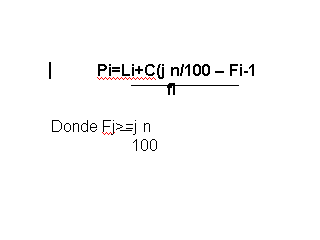
Los percentiles, deciles y cuartiles corresponden a medidas de posición, pero no de tendencia central.
Hemos visto que la mediana divide a al muestra en partes iguales.
Percentiles:
Son los 99 valores que dividen la distribución en 100 partes iguales se designan por P1, P2...P99, donde P1 es el percentil 1, P2 es el percentil 2, etc. El P50 coincide con la mediana.
Ejemplo1:
En una distribución de notas de alumnos el percentil P46 es una nota de referencia que permite afirmar que el 46% de esos alumnos obtuvo esa nota o una menor.
El cálculo del percentil es similar al cálculo de la mediana:
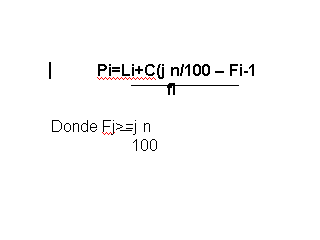
Ejemplo2:
La siguiente distribución de alumnos presenta los puntajes obtenidos en la
prueba de estadística:
| Yi-1 Yi | fi | FI |
|---|---|---|
| 10-20 | 7 | 7 |
| 20-30 | 3 | 10 |
| 30-40 | 15 | 25 |
| 40-50 | 10 | 35 |
| 50-60 | 6 | 41 |
| 60-70 | 5 | 46 |
| 70-80 | 6 | 52 |
Calcualremos el percentil 40:
N=52 j*n/100=40*52/100=20.8 y Fi>=20.8 es F3=25 y Li=30, Fi-1=10, fi=15,
C=10
Reemplazando estos valores en la fórmula

El 40 por ciento de los alumnos obtuvo puntajes menores o iguales a 37.2
Cuartiles:
Los percentiles 25,50,75 reciben el nombre de cuartiles y se simbolizan con la letra Q. Por tanto tenemos:
P25=Q1, P50=Q2, P75=Q3
Se puede observar que el cuartil dos (Q2) es igual al percentil 50 (P50), el cual corresponde a la definición de mediana.
Los cuartiles dividen a la distribución en cuatro partes iguales, por lo tanto hay tres cuartiles Q1, Q2, Q3.
El cálculo de los cuartiles es similar al de los percentiles:

Ejemplo:
Determinar los cuartiles para la distribución anterior e interpretar el resultado:
Para Q1 se tiene:
Fj>=n/4 Luego Fj>= 52/4 Y Fj= 25, Lj= 30 , Fj-1= 10, C=10, fj=15

Esto quiere decir que el 25% de los alumnos obtuvo puntaje menor o igual a 32


Esto quiere decir que el 50% de los alumnos obtuvo puntaje menor o igual a 41

Esto quiere decir que el 75% de los alumnos obtuvo puntaje menor o igual a 56,57
Deciles:
Son aquellas variables que dividen a una distribución en 10 partes iguales, por lo tanto hay 9
deciles.
El decil 5 (D5) coincide con la mediana y con el segundo cuartil, es decir D5= Me=Q2
El cálculo de los Deciles es similar al de los Cuartiles y Percentiles.

Por ejemplo :

Ejemplo:
Para el ejemplo de los puntajes de los alumnos en estadística, calcular D5 e interpretar el resultado
Para calcular D5 tenemos que:
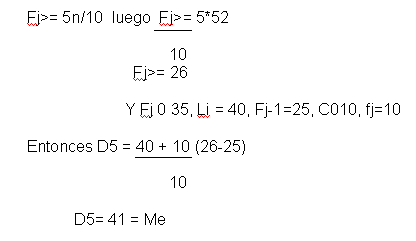
El quinto decil coincide con la mediana
Esto quiere decir que el 50% de los alumnos obtuvo puntaje menor o igual a 41 puntos